Pattern formation
A pattern is an arrangement of objects displaying mathematical, geometric or statistic relationships (e.g., atoms organized in molecules, and molecules that in a big scale can form crystals). In swarm robotics, robots can form patterns by strategically positioning themselves in regard to the position of other robots they perceive. By following simple positioning rules at the individual level, a robot swarm can distributed itself in the form of organized structures.
Robot pattern formation is useful to perform tasks such as uniformly covering a region of interest, establishing specific lattice or network topologies, and performing collective motion (known as flocking in the context of swarm robotics).
Objective
The objective of this practical session is to design the control software for a robot swarm that exhibits pattern formation and flocking behaviors.
General remarks
The control software of the robots is executed in the form of time steps—that is, the script is executed in the simulator once for each time step. In this experiment, the time step has a length of 100ms. In other words, each of the actions defined in the Lua script will be executed 10 times per second.
It is expected that you use the control software produced in practical session (P2.2) to allow the robots to detect and localize their peers.
Remember that the individual actions of each robot are the ones that lead the robot swarm to achieve the desired behavior.
Exercise 1: Hexagonal pattern formation
In this exercise, you will use the notion of artificial potential fields to form hexagonal patterns with a swarm of foot-bots.
Launching the experiment
1 - Enter the directory that contains the materials for this practical session.
cd ~/swarm_robotics/pattern_formation/
2 - Run the ARGoS simulation.
argos3 -c pattern_formation.argos
Experimental setup
At the beginning of the experiment, a swarm of foot-bots is randomly distributed in a rectangular bounded arena. During the execution of the experiment, the robots must position themselves so that the inner structure of the swarm can be appreciated as an hexagonal lattice. The experiment will end when all robots are formed and the lattice remains stable.
Artificial potential fields
Artificial potential fields are computing models that emulate the effects of physical potential fields such as electrical, magnetic or gravitational fields. In robotics, artificial potential fields can be used to model virtual forces to which a robot is subject. This forces can represent attraction or repulsion behaviors that lead the robot motion; for example, they can be computed in regard to the position of other robots or objects in the environment.
In swarm robotics, researchers have widely used the Lennard-Jones potential to create virtual forces that enable the formation of patterns with robot swarms. A robot is subject to virtual attraction and repulsion forces that aim to maintain a target distance with respect to nearby robots. The robot is attracted to robots that are farther than the target distance, and on the contrary, it is repealed from robots that are closer. A stable state will be reached when the robot finds a position in which it maintains the target distance with respect to all its nearby peers.
The image below represents the Lennard-Jones potential and indicates the distribution of the forces with respect to the target distance.
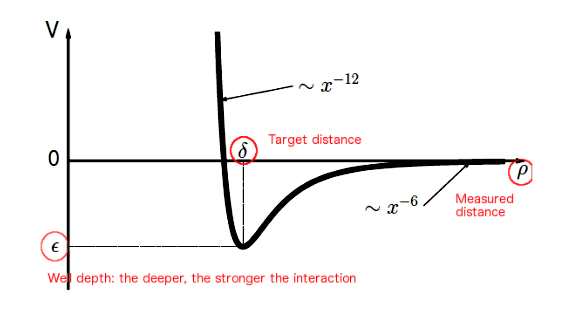
In the graph above, delta is the target distance to be maintained, rho is the distance measured against the position of other robot, and epsilon indicates the strength of the interaction.
The potential is described by the expression,
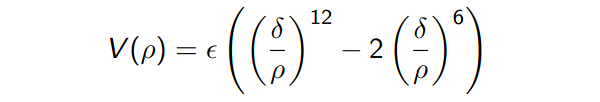
The corresponding forces can be obtained after applying the firs derivative,
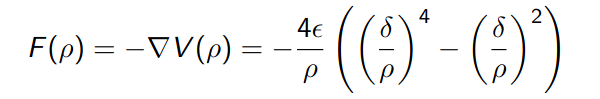
Controller description
In this exercise, you are provided with a starting Lua script that contains a few constant declarations and functions that will facilitate the development of the control software. Your task is to develop the rest of the script.
The basic control pseudocode is summarized below.
1 - Compute the force due to Lennard-Jones potential
for each robot i seen at {range_i, bearing_i}
do
ln_value = ComputeLennardJones(range_i)
Set a 2D vector vec[i] according to {ln_value, bearing_i}
ln_force += vec[i]
end
2 - Compute the direction of movement
mov_dir = GetAngle(ln_force)
3 - Set the robot velocity
Velocity{l,r} = ComputeSpeedFromAngle(mov_dir)
The function ComputeSpeedFromAngle() is provided and described in the starting script.
Proposed solution
A proposed solution for the exercise will be available to download after midnight.
Exercise 2: Circular pattern formation
In this exercise, you will combine virtual forces originated by inter-robot interaction with a virtual force originated by an object of the environment.
Launching the experiment
1 - Enter the directory that contains the materials for this practical session.
cd ~/swarm_robotics/pattern_formation/
2 - Run the ARGoS simulation.
argos3 -c pattern_formation.argos
Experimental setup
At the beginning of the experiment, a swarm of foot-bots is randomly distributed in a rectangular bounded arena that contains one small red LED. During the execution of the experiment, the robots must position themselves so that the robot swarm forms a circular pattern around the red LED. The experiment will end when all robots are formed and the lattice remains stable.
Controller description
In this exercise, you can start from the code that you developed in the Exercise 1. Your task is to extend the script so that the robots form around the LED.
The basic control pseudocode is summarized below. Bear in mind that the LEDs just display color signals, and such signals can be perceived only by the omnidirectional camera. Further information about how to use the LEDs and the omnidirectional camera is provided in the section the foot-bot.
1 - Compute the force due to Lennard-Jones potential
2 - Compute the attractive force towards the LED at {range_led, bearing_led}
Set a 2D vector vec_led according to {range_led, bearing_led}
led_force = vec_led
3 - Aggregate the forces
sum_force = ln_force + led_force
4 - Compute the direction of movement
mov_dir = GetAngle(sum_force)
5 - Set the robot velocity
Proposed solution
A proposed solution for the exercise will be available to download after midnight.
Exercise 3: Flocking
In this exercise, you will create a swarm that flocks—that is, a swarm that moves while forming a pattern.
Launching the experiment
1 - Enter the directory that contains the materials for this practical session.
cd ~/swarm_robotics/pattern_formation/
2 - Run the ARGoS simulation.
argos3 -c pattern_formation.argos
Experimental setup
At the beginning of the experiment, a swarm of foot-bots is randomly distributed in a rectangular bounded arena that contains one small red LED and one ambiance light source. During the execution of the experiment, the robots must position themselves so that the inner structure of the swarm can be appreciated as an hexagonal lattice. The experiment will end when all robots are formed and the lattice remains stable.
Controller description
In this exercise, you can start from the code that you developed in the Exercise 2. Your task is to extend the script so that the robots move towards the ambiance light source after they are formed around the LED. Note that you will need to design a triggering condition that causes a behavior change in the robot: they need to stop being attracted to the LED and start being attracted to the ambiance light source.
The basic control pseudocode to drive the robots towards the ambiance light source is summarized below.
1 - Compute the force due to Lennard-Jones potential
2 - Compute the attractive force towards the ambiance light source at {range_light, bearing_light}
{range_light, bearing_light} = ComputeVectorToLight()
Set a 2D vector vec_light according to {range_light, bearing_light}
light_force = vec_light
3 - Aggregate the forces
sum_force = ln_force + light_force
4 - Compute the direction of movement
5 - Set the robot velocity
Proposed solution
A proposed solution for the exercise will be available to download after midnight.
Further readings
The following reading shows an interesting experiment in which a robot swarms uses pattern formation to escort a human in virtual hazardous scenarios.
